http://www.education.com/study-help/article/pre-calculus-help-conics-ellipses/
1) Ellipse: "The set of all points such that the sum of the distance from two points is a constant." (Taken by Mrs. Kirch's SSS Packet)
2)

2)

(http://imanawkwardturtle.files.wordpress.com/2013/03/hyperbolas3.png)
The formula for an Ellipse is (x-h)^2/a^2 + (y-k)^2/b^2 =1 or (x-h)^2/b^2 + (y-k)^2/a^2 =1The formula of an ellipse can be determined depending what number is bigger on the denominator. As you see in the image below, if the denominator is bigger under the (x-h)^2, then you will know that your graph will be "fat" or "wide" horizontally. If the denominator is bigger under the (y-k)^2, then you will know that your graph will be "skinny" or "tall" vertically.
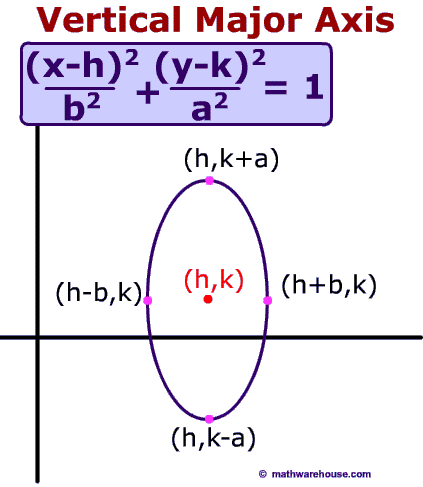
(http://www.mathwarehouse.com/ellipse/images/translations/general_formula_major.gif)
As you can see from the picture above, the ellipse is skinny/tall so you will know that it is vertical.
Horizontal Major Axis

(http://image.tutorvista.com/content/feed/u1989/hoe%20ellipse.GIF)
As you can also see from the above picture, the ellipse is fat/short, so you will know that it is horizontal.
The key features in an ellipse is the standard form, center, skinny or fat, "a=", "b=", "c=", 2 vertices, 2 co-vertices, 2 foci, major axis, minor axis, eccentricity, and the graph.
-To get the standard form of an ellipse you need to complete the square, after you do that, divide everything from the other side to the variables so it can equal to one. After getting your standard form, you look at the denominators of (x-h)^2 and (y-k)^2, and if a^2 is bigger under "x" your graph will be fat, and if the denominator is bigger under "y" then it will be skinny.
-To get your center, you look at (x-h)^2 and (y-k)^2, you equal them to zero, and you get your center. "a=" will always be bigger than "b=", so you look at (x-h)^2 and (y-k)^2, and you square root their denominators; the biggest number is "a=" and the smallest is "b=". To get your "c=", you can use the equation "a^2-b^2=c^2", you plug in the numbers and after you square root the end, you get "c=".
-Your major axis will be the numerator equal to zero, that has the smallest denominator. While the minor axis will be the numerator equal to zero, that has he biggest denominator.
-To get your 2 vertices, you add and subtract the "a=" to the center point of either "x" or "y", depending what the major axis is. To get your 2 co-vertices, you add and subtract the "b=" to the center point of either "x" or "y", depending on what your minor axis is. To get the 2 foci, you put your minor axis and add and subtract to what "c=" and you leave the major axis by itself.
-To get your eccentricity, you use the equation "e=c/a" and you plug in the numbers and you will get your eccentricity, but remember to have it in the thousands place.
-To get your graph, you plug everything that you found, but to remember to use a solid line to show that it is your major axis and to use a dotted line for the minor axis, your foci will always be inside the ellipse, your vertices and co-vertices will be its boundaries, and the shape of your ellipse will match up with either skinny or fat, and your center will be in the middle. The bigger the ellipse, the farther the foci will be, but the closer the ellipse is, the closer the foci is. The foci is the same distance to any point in the ellipse.The foci affects the eccentricity because it determines the shape of the ellipse and how close it is to the ellipse's eccentricity, which equals one.
-To get the standard form of an ellipse you need to complete the square, after you do that, divide everything from the other side to the variables so it can equal to one. After getting your standard form, you look at the denominators of (x-h)^2 and (y-k)^2, and if a^2 is bigger under "x" your graph will be fat, and if the denominator is bigger under "y" then it will be skinny.
-To get your center, you look at (x-h)^2 and (y-k)^2, you equal them to zero, and you get your center. "a=" will always be bigger than "b=", so you look at (x-h)^2 and (y-k)^2, and you square root their denominators; the biggest number is "a=" and the smallest is "b=". To get your "c=", you can use the equation "a^2-b^2=c^2", you plug in the numbers and after you square root the end, you get "c=".
-Your major axis will be the numerator equal to zero, that has the smallest denominator. While the minor axis will be the numerator equal to zero, that has he biggest denominator.
-To get your 2 vertices, you add and subtract the "a=" to the center point of either "x" or "y", depending what the major axis is. To get your 2 co-vertices, you add and subtract the "b=" to the center point of either "x" or "y", depending on what your minor axis is. To get the 2 foci, you put your minor axis and add and subtract to what "c=" and you leave the major axis by itself.
-To get your eccentricity, you use the equation "e=c/a" and you plug in the numbers and you will get your eccentricity, but remember to have it in the thousands place.
-To get your graph, you plug everything that you found, but to remember to use a solid line to show that it is your major axis and to use a dotted line for the minor axis, your foci will always be inside the ellipse, your vertices and co-vertices will be its boundaries, and the shape of your ellipse will match up with either skinny or fat, and your center will be in the middle. The bigger the ellipse, the farther the foci will be, but the closer the ellipse is, the closer the foci is. The foci is the same distance to any point in the ellipse.The foci affects the eccentricity because it determines the shape of the ellipse and how close it is to the ellipse's eccentricity, which equals one.
3) (https://www.youtube.com/watch?v=lvAYFUIEpFI)
Conics of ellipses can be seen in buildings or statues around the world, but it helps find the height and length of it. The foci that are plugged in can determine what kind of eccentricity you would want as the outcome. Ellipses can be seen in power plants, buildings, statues, basketballs, car logos, and many more things. Just like it says in the video, you can determine your ellipse by putting in what it gives you. You can use what they give you, and you can slowly get the other parts when you connect everything together and do it step by step.

(http://ww1.prweb.com/prfiles/2009/11/19/248313/EllipseofFire.jpg)
-A fun example I will use is the the picture of the eye above. (If you know about the difference about single and double eyelids, then you can comprehend this example easily). Referencing its shape, you can see it as an "single-eyelid eye" or a "double eyelid eye". If the eye has a single-eyelid, you can infer that it is small so its foci would be closer. On the other hand, if the eye has a double-eyelid look, then you can infer that the eye is bigger, so its foci will be farther apart.
Conics of ellipses can be seen in buildings or statues around the world, but it helps find the height and length of it. The foci that are plugged in can determine what kind of eccentricity you would want as the outcome. Ellipses can be seen in power plants, buildings, statues, basketballs, car logos, and many more things. Just like it says in the video, you can determine your ellipse by putting in what it gives you. You can use what they give you, and you can slowly get the other parts when you connect everything together and do it step by step.

(http://ww1.prweb.com/prfiles/2009/11/19/248313/EllipseofFire.jpg)
-A fun example I will use is the the picture of the eye above. (If you know about the difference about single and double eyelids, then you can comprehend this example easily). Referencing its shape, you can see it as an "single-eyelid eye" or a "double eyelid eye". If the eye has a single-eyelid, you can infer that it is small so its foci would be closer. On the other hand, if the eye has a double-eyelid look, then you can infer that the eye is bigger, so its foci will be farther apart.
4) Work Cited:
- Mrs. Kirch's Unit M SSS Packet
- http://ww1.prweb.com/prfiles/2009/11/19/248313/EllipseofFire.jpg
- https://www.youtube.com/watch?v=lvAYFUIEpFI
- http://www.education.com/study-help/article/pre-calculus-help-conics-ellipses/
- http://imanawkwardturtle.files.wordpress.com/2013/03/hyperbolas3.png
- http://www.mathwarehouse.com/ellipse/images/translations/general_formula_major.gif
- http://image.tutorvista.com/content/feed/u1989/hoe%20ellipse.GIF
No comments:
Post a Comment